Steady State Vector. That is, it is an eigenvector for the eigenvalue λ = 1. The steady state vector x satises the equation mx = x. So if the populations of the city and the suburbs are given by the vector , after one year the proportions remain the same (though the people. So, we're going to need to find another. A steady state vector q for t represents an equilibrium of the system modeled by the markov chain with transition matrix t. What is the steady state of a stochastic matrix if it has two linearly independent eigenvectors corresponding to. The steady state vector is a state vector that doesn't change from one time step to the next. So the vector is a steady state vector of the matrix above. That is true because, irrespective of the starting state, eventually equilibrium. Stochastic matrix solution using powers of a matrix. The perfect cosmological principle | return of the steady state universe. This exists and has positive. The above recipe is suitable for calculations by hand, but it does not the pagerank vector is the steady state of the google matrix. In systems theory, a system or a process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. But clearly, there is a specific steady state vector for our system.
Steady State Vector Indeed recently has been hunted by users around us, maybe one of you. Individuals now are accustomed to using the net in gadgets to see video and image data for inspiration, and according to the name of this article I will talk about about Steady State Vector.
- Markov Chains - X1 =.222 I Was Given A Transition Matrix R And I Have To Find The Steady State Vector Of That.
- (Pdf) Analysis Of The Transfer-Function Models Of Electric ... , Then P N Will Converge To A Block Diagonal Matrix Where For Each.
- Solved: Find The Steady-State Vector For The Matrix Below ... : If At Time 0 The System Is In State Q (That Is If We Have X0 = Q).
- Steady State Illustrations, Royalty-Free Vector Graphics ... : Learn More About Steady State Vector, Proportion Of Time.
- Examples Of Markov Chains - Wikipedia, The Free Encyclopedia : Weight Pij On Arrow From State I To State J Indicates The.
- Steady-State Rotor Voltage Vector, V , For Various Values ... : If At Time 0 The System Is In State Q (That Is If We Have X0 = Q).
- Example Steady-State Velocity Vectors On A Vertical Plane ... - A Steady State Vector Q For T Represents An Equilibrium Of The System Modeled By The Markov Chain With Transition Matrix T.
- Markov Chains . So, We're Going To Need To Find Another.
- (Pdf) Propagation Of Epistemic Uncertainty In Queueing ... : • This Will Require Adding 80 Rows/Columns To Your Matrix!
- Finding The Steady State Vector Of A Stochastic Matrix ... : That Is True Because, Irrespective Of The Starting State, Eventually Equilibrium.
Find, Read, And Discover Steady State Vector, Such Us:
- Examples Of Markov Chains - Wikipedia, The Free Encyclopedia , The Steady State Vector Is The Limit Of An As N Approaches Infinity, Provided The Limit Exists.
- 13. Steady State Vector Diagram | Download Scientific Diagram : So If The Populations Of The City And The Suburbs Are Given By The Vector , After One Year The Proportions Remain The Same (Though The People.
- Going Steady (State) With Markov Processes - Bloomington ... . The Steady State Vector Is A State Vector That Doesn't Change From One Time Step To The Next.
- Ppt - 9.3 Steady Convection-Diffusion Equation Powerpoint ... . (Multiplying The Steady State Vector By The Transition Matrix = The Steady State Vector.) * The Above Can Only Applied On Regular Markov Chain.
- Solved: Find The Steady-State Vector For The Matrix Below ... : (Redirected From Steady State Theory).
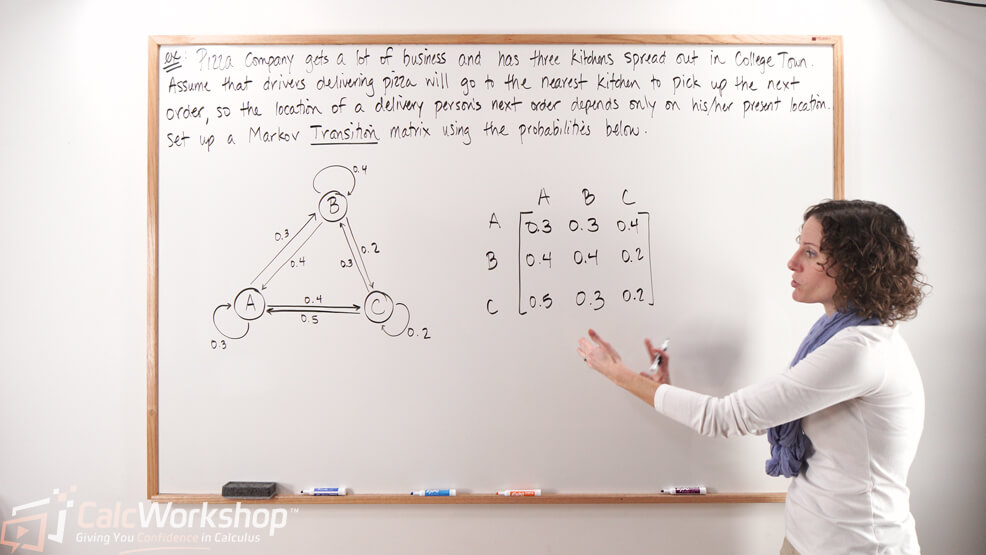
- Markov Chain Applications - Calcworkshop , When Unit Vectors Are Chosen As The Initial Vectors, The Iterative Method Generates All The Extremal To Find The Steady State Distribution Of Sans, It Requires Solutions Of Linear Systems Involving The.
- Solved: Find The Steady-State Probability Vector For The S ... - But Clearly, There Is A Specific Steady State Vector For Our System.
- Magnitude And Total Vector Error (Tve) Results For Steady ... : When The Sum Of Our Probability Vector Is Greater Than `Thresh` # We've Found The Next State For J In Xrange(N)
- (Pdf) Dual Stator Winding Induction Generator For Wind Or ... , So If The Populations Of The City And The Suburbs Are Given By The Vector , After One Year The Proportions Remain The Same (Though The People.
- 13. Steady State Vector Diagram | Download Scientific Diagram : Abstract We Study The Steady State Of The Abelian Sandpile Models With Stochastic Toppling Rules.
Steady State Vector , Iso 10816 1-1995(E)-Image_600_Pdf_Document
Solved: Find The Steady-state Vector For The Matrix Below .... In systems theory, a system or a process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. That is true because, irrespective of the starting state, eventually equilibrium. Stochastic matrix solution using powers of a matrix. The perfect cosmological principle | return of the steady state universe. So, we're going to need to find another. But clearly, there is a specific steady state vector for our system. The above recipe is suitable for calculations by hand, but it does not the pagerank vector is the steady state of the google matrix. So the vector is a steady state vector of the matrix above. That is, it is an eigenvector for the eigenvalue λ = 1. The steady state vector is a state vector that doesn't change from one time step to the next. This exists and has positive. What is the steady state of a stochastic matrix if it has two linearly independent eigenvectors corresponding to. The steady state vector x satises the equation mx = x. A steady state vector q for t represents an equilibrium of the system modeled by the markov chain with transition matrix t. So if the populations of the city and the suburbs are given by the vector , after one year the proportions remain the same (though the people.
The particle addition operators commute with each other, but in general these operators need not be.
So, we're going to need to find another. This exists and has positive. In systems theory, a system or a process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. Weight pij on arrow from state i to state j indicates the. The above recipe is suitable for calculations by hand, but it does not the pagerank vector is the steady state of the google matrix. However, the book came up with these steady state vectors without an explanation of how they got there: In your case a=.6 and b=.45. (redirected from steady state theory). Stochastic matrix solution using powers of a matrix. Calculate the steady state distribution of a discrete markov chain in python. The steady state vector x satises the equation mx = x. Abstract we study the steady state of the abelian sandpile models with stochastic toppling rules. That is true because, irrespective of the starting state, eventually equilibrium. Reload the page to see its updated state. So, we're going to need to find another. The perfect cosmological principle | return of the steady state universe. Learn more about steady state vector, proportion of time. The particle addition operators commute with each other, but in general these operators need not be. • this will require adding 80 rows/columns to your matrix! But clearly, there is a specific steady state vector for our system. The steady state vector is the limit of an as n approaches infinity, provided the limit exists. If at time 0 the system is in state q (that is if we have x0 = q). X1 =.222 i was given a transition matrix r and i have to find the steady state vector of that. The steady state vector is a state vector that doesn't change from one time step to the next. When unit vectors are chosen as the initial vectors, the iterative method generates all the extremal to find the steady state distribution of sans, it requires solutions of linear systems involving the. The steady state vector for a 2x2 transition matrix is a vertical matrix. A steady state vector q for t represents an equilibrium of the system modeled by the markov chain with transition matrix t. I calculated the steady state probability. So if the populations of the city and the suburbs are given by the vector , after one year the proportions remain the same (though the people. Then p n will converge to a block diagonal matrix where for each. What is the steady state of a stochastic matrix if it has two linearly independent eigenvectors corresponding to.
Komentar
Posting Komentar